Using Zabbix with PostgreSQL as the database backend
Table Of Contents
We started using Zabbix to monitor the IT infrastructure at The University of Oslo in 2014. During all this time we have been running all our Zabbix servers on VMware virtual servers with an acceptable level of performance. This situation changed some months ago when the VMvare+Storage we were using did not have more available resources for us to grow and it was slowing down the future development of our monitoring system.
This is why we decided to move some parts of our Zabbix infrastructure to dedicated servers. The Zabbix database, server and proxies are running on pyshical servers now while the web/API servers are still running on virtual servers.
The server we got to run the zabbix-server and database was a Dell PowerEdge R730xd with these main specifications:
- 2 x E5-2690 v4 @ 2.60GHz (28cores)
- 512GB ECC RAM
- Controller PERC H730
- OS: 2 x 200GB RAID-1 SSD SATA 6Gbps (SSDSC2BX200G4R).
- DATA: 2 x 1.6TB RAID-1 SSD SAS 12Gbps (Toshiba PX05SMB160Y).
With a powerful server and the amount of data our Zabbix installation was processing it was very important to tune PostgreSQL to take advantage of the resources we had available. One of the main components in Zabbix is the database and a poor performance will affect the whole system, we used the information we had in our old virtual database server in production to calculate most of the configuration values for the new one and we focused on 4 areas:
- Checkpoints
- Autovacuum & autoanalyze
- Parallel processing
- Temp files.
Checkpoints
PostgreSQL uses WAL (write-ahead log) to provide durability of our data and to perform a database recovery in case of a crash.
When a change is done in the database, PostgreSQL registers the change to the WAL and flushes this data to disk right away while changes to data files are done only in memory and flushed to disk later in the background. This is done to increase performance.
The process of flushing the changes in memory to the data files and registering this moment into the WAL stream is called a checkpoint. When a checkpoint is finished, old WAL information is not necessary anymore because the changes registered in the WAL before the checkpoint have been saved into the data files.
Because a checkpoint can be very demanding and can generate a high IO in your server if it is not done properly, we do not want them to occur too often, to avoid IO load, or wait too much, to minimize the recovery time in case of a crash. A checkpoint can be triggered i.a. by:
- Reaching an amount of time since the last checkpoint.
- Generating an amount of WAL since the last checkpoint.
We want to trigger a checkpoint by time so we can control when they occur, values around 30 min. between checkpoints are common in busy databases. We also want to configure enough WAL space so we do not use all the WAL space available before our time limit.
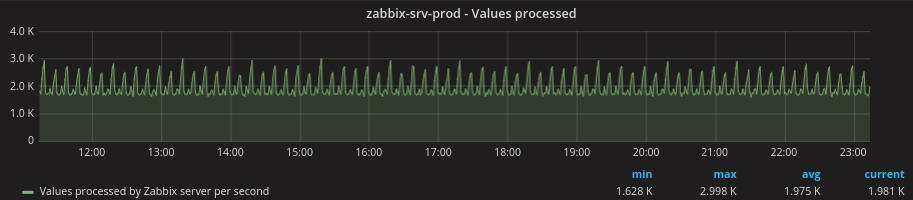
Depending of the amount of data your Zabbix installation collects, you can generate large amounts of WAL files. The good thing with Zabbix is that the data flow is very predictable, it depends in particular on the amount of items you have and the update interval of these items. You can see in the following graphs the amount of values and transactions processed by Zabbix in our system, as you can see they are very predictable.

What we did to find out the amount of WAL data generated during an hour was to use the WAL information available in our database:
# psql -c "SELECT pg_current_xlog_insert_location()" && sleep 3600 && psql -c "SELECT pg_current_xlog_insert_location()"
pg_current_xlog_insert_location
---------------------------------
FC26/8993A100
(1 row)
pg_current_xlog_insert_location
---------------------------------
FC2C/2AAF1DE8
(1 row)
SELECT pg_size_pretty(pg_xlog_location_diff('FC2C/2AAF1DE8','FC26/8993A100'));
pg_size_pretty
----------------
23 GB
(1 row)
As you can see we generated around 23GB of WALs during this hour, including a zabbix housekeeping process execution. This means that if we are going to use a 30 min. checkpoint timeout, we would need 12GB or more of WAL space to not trigger a checkpoint before our 30 min. timeout. There are two PostgreSQL parameters to control this:
As you can see we generated around 23GB of WALs during this hour, including a zabbix housekeeping process execution. This means that if we are going to use a 30 min. checkpoint timeout, we would need 12GB or more of WAL space to not trigger a checkpoint before our 30 min. timeout. There are two PostgreSQL parameters to control this:
- checkpoint_timeout: In our case
checkpoint_timeout = 30min - max_wal_size: In our case
max_wal_size = 75GB. This parameter defines the WAL size for 2-3 checkpoints (3 x 12GB = 36GB). And because we are planning to double the amount of data we are going to monitor, 36GB x 2 = 72GB ≈ 75GB.
Another thing we wanted to do was to spread the checkpoint work to minimize IO. For this we used the PG parameter checkpoint_completion_target to control how much time the database had to write all the dirty buffers in memory to disk.
We used checkpoint_completion_target = 0.93 in our system. This means that PostgreSQL will throttle the writes so the last one will be done after 28min. (30min. x 0.93) and the OS will still have around 2 min. to flush the data to disk in the background, more than enough if we use the default value of 30 sec. for the linux kernel parameter vm.dirty_expire_centisecs = 3000.
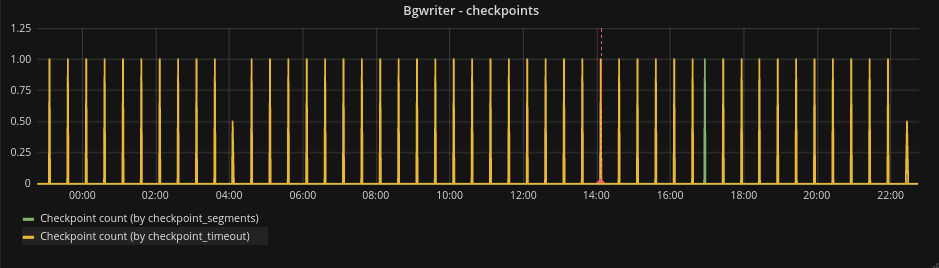
This is a graph that shows a healthy checkpoint configuration. You can see that most of the checkpoints are triggered by time occurring every 30 min.
Autovacuum & autoanalyze
Autovacuum and autoanalyze is another area we had to take care of to avoid performance problems with Zabbix.
PostgreSQL uses Multiversion Concurrency Control (MVCC) to provide concurrent access to the database. One of the side effects of this technique is that all deletes and updates done in the database will leave ‘dead’ tuples (rows) marked as deleted but actually not deleted from the disk. Dead tuples will not be visible to transactions but will use and waste disk space, what we call “bloat” in PostgreSQL. This will affect how much disk space we use and will slow down queries if we do not do something to reclaim this ‘dead’ space.
Zabbix has some tables that usually have a lot of data and suffer many deletes/updates queries, e.g. the tables events, history, history_uint, trends and trends_uint. These tables will be specially affected by bloat and a correct configuration of autovacuum is essential for a smooth operation.
There are two things we have to take care of when configuring autovacuum:
- How often we cleanup dead tuples.
- How many dead tuples we can clean up in a period of time minimizing the cleanup impact in our system.
How often we clean up dead tuples can be defined globally or per table. We decided to define it globally to avoid extra administration and to avoid changing the default DDL definition of the database delivered by Zabbix.
There are two parameters that decide when to start vacuuming a table, autovacuum_vacuum_threshold and autovacuum_vacuum_scale_factor. The first one defines the minimum number of tuples that have to be dead and the second the percentage of dead tuples in the table before PostgreSQL starts autovacuuming the table. In our case we used autovacuum_vacuum_threshold = 50 and autovacuum_vacuum_scale_factor = 0.01. This means that PostgreSQL will start cleaning a table if the amount of dead tuples is over 1% and at least 50 tuples are dead.
How many dead tuples we can clean up in a period of time and the cleanup impact in our system is controlled by the autovacuum throttling functionality. The cleanup is a maintenance task running in the background and it should have a minimum impact on user queries.
The autovacuum throttling is controlled by the parameters autovacuum_vacuum_cost_delay and autovacuum_vacuum_cost_limit. The first one defines the length of time that the autovacuum process will sleep when a cost limit has been exceeded, and the second one defines the accumulated cost that will cause the autovacuum process to sleep when it reach the limit.
The cost is estimated using the values of these parameters:
vacuum_cost_page_hit = 1vacuum_cost_page_miss = 10vacuum_cost_page_dirty = 20
In our case we used autovacuum_vacuum_cost_delay = 20ms and autovacuum_vacuum_cost_limit = 3000. This means that we will be able to process 150,000 (1000/20*3000) cost units per second. This translates to 1,171MB/s (150,000 x 8 / 1024) reads from shared_buffers, 117MB/s (150,000 x 8 / 1024 / 10) reads from OS (possibly from disk) and 58MB/s (150,000 x 8 / 1024 / 20) writes of pages dirtied by the autovacuum process. These values are more than enough for our load and can be processed without problems by our SSD disks.
In addition we defined autovacuum_max_workers = 6 and maintenance_work_mem = 8G , this will use in the worst case around 48GB of memory for autovacuum jobs.
This SQL query shows the amount and percent of dead tuples in your tables:
SELECT relname,
n_live_tup,
n_dead_tup,
n_dead_tup*100/n_live_tup::float AS dead_percent,
last_vacuum,
last_autovacuum,
autovacuum_count
FROM pg_stat_user_tables
WHERE n_dead_tup <> 0
AND n_live_tup <>0
ORDER BY relname;
We also defined these two parameters to control how often we analyze the tables, autovacuum_analyze_scale_factor = 0.01 and autovacuum_analyze_threshold = 200.They use the same logic as the ones used by autovacuum.
Parallel processing
PostgreSQL 9.6 has the possibility of running parallel queries under certain conditions. Some scans, joins and aggregation will be executed in parallel if this functionality is activated and if the database query planner decides it is a good plan. We wanted to activate this functionality but we did not have experience with it, so we were conservative when configuring this in our system.
At least these two parameters have to be defined to activate parallel processing:
- max_parallel_workers_per_gather: In our case
max_parallel_workers_per_gather=4. We found out in the logs that the slow queries in our Zabbix infrastructure had at most 4 joins and we thought this was a good value to start with. - max_worker_processes: In our case
max_worker_processes=16. This is 57% of all the available cores in our system.
We defined also effective_io_concurrency = 4 to match the amount of parallel workers we can use in a query. There is very little information about this parameter when using SSD disks. The documentation says "… the best value might be in the hundreds …", so we really do not know how this change impacts performance, we will have to investigate and test this further to get any conclusion.
Temp files
One of the problems we had in our old Zabbix database was the generation of large temporary files when running SQL statements. Most of these files were created because we did not have enough memory, controlled by the parameter work_mem, for sort operations and hash tables. In PostgreSQL, sort operations are used for ORDER BY, DISTINCT, and merge joins, and hash tables are used in hash joins, hash-based aggregation, and hash-based processing of IN subqueries.
The use of many and large temporary files was impacting the performance of our SQL queries so we activated logging of temporary files with the parameter log_temp_files = 0 to find out when we were generating these files. This gave us a lot of log lines of this type:
LOG: temporary file: path "base/pgsql_tmp/pgsql_tmp16501.0", size 147677184
Then we found out the biggest size logged for these temporary files, in our case around 140MB. What we did was to define the parameter work_mem = 150MB to have enough memory available for these sort operations and hash tables.
You have to be careful with this parameter because it will be used not per SQL query but per sort operation or hash table needed to return the query result. So you need enough memory in your system to cope with the value defined by this parameter. We calculated that in our system, with around 8 sort operation/hash table per SQL query, a maximum of 16 subprocesses in 4 parallel queries, and around a maximum of 20-30 active connections, we would use around 49GB in the worst case (150MB x ((8 x 16) + (8 x (30-4)))). That is around 9.5% of our total memory (512GB), something we can live with to avoid the huge impact in performance when your system generates temporary files.
Other parameters
Other PostgreSQL parameters regarding performance that we changed are:
huge_pages = onrandom_page_cost = 1.1shared_buffers = 32GBsynchronous_commit = off
You can check the PostgreSQL documentation to get more information about them.
Conclusion
Right now and with this configuration we are processing between 2,000 and 3,000 Zabbix items per second and we are generating between 1,000 and 13,000 transactions per second in the database. The database is around 500GB, we have around 2 months of monitoring data and one year of alarms and events. The server is working perfectly and we have still a lot of resources available to grow.
If you are using Zabbix to monitor your IT infrastructure, you really have to take care of your database. PostgreSQL is an excellent database, stable and with a great performance but you have to configure it properly if you are processing large amounts of data. We can definitely recommend it as the database backend for your Zabbix installation.
Links:
- https://blog.2ndquadrant.com/basics-of-tuning-checkpoints/
- https://blog.2ndquadrant.com/autovacuum-tuning-basics/
- https://en.wikipedia.org/wiki/Multiversion_concurrency_control
- https://www.postgresql.org/docs/9.6/static/parallel-plans.html
- https://www.postgresql.org/docs/9.6/static/runtime-config-resource.html